[Thảo luận] Thuật toán

[toannv]

1 năm club thuật toán chưa có đến nổi 10 hoạt động nữa

Em có thể lên các trang thi online mà thấy MSSV của UIT là .. "nó" đó.

[14520103]

1 năm club thuật toán chưa có đến nổi 10 hoạt động nữa

[08520001]

Bài của Tín có vẻ khó đây. Nếu làm bình thường, xét lần lượt từ trái qua phải tất cả các dãy con N - K 1 phần tử, với mỗi dãy con, duyệt K phần tử của dãy con đó và tìm phần tử nhỏ nhất, thì độ phức tạp là O(N * K) có thể chạy được nếu giới hạn thời gian 5s.

[12520527]

[MENTION=11756]11520246[/MENTION] : có thể áp dụng như cách anh đề cập để luyện kĩ năng chia nhị phân :smile:
Có vẻ như trường mình không mấy ai hào hứng với những bài toán tin như thế này nhỉ udency:
Để hâm nóng lại topic, em xin góp củi thêm một bài :salute:

Cho 2 số nguyên dương N, K (K <= N) và một dãy A gồm N phần tử là các số nguyên dương. Xét lần lượt N - K + 1 dãy con gồm K phần tử liên tiếp trong dãy đã cho (dãy con thứ nhất là A[1...K], dãy con thứ hai là A[2..K+1] ...), với mỗi dãy con hãy in ra phần tử có giá trị bé nhất trong dãy con đó.
Giới hạn : N <= 20000.

Ví dụ :
N = 4, K = 2
Dãy A : 3 2 4 1

Dãy con thứ nhất : 3 2 -> Phần tử bé nhất (PTBN) : 2
Dãy con thứ hai : 2 4 -> PTBN : 2
Dãy con thứ ba : 4 1 -> PTBN : 1

--> Output sẽ là 2 2 1

[11520246]

[MENTION=7969]09520019[/MENTION] Anh ơi, em đã rõ hơn rồi ạ, lúc trước em nhìn vào phương trình bài toán ban đầu: a^3 + b^3 + c^3 = 100a + 10b + c rồi lại nghe anh chuyển vế lấy cái đống kia làm hằng với 2 ẩn tự do là a và b, và rồi chỉ việc đi tìm c nên thấy hơi ngợp và thắc mắc rằng a,b lấy ở đâu ra mà bảo làm ẩn tự do gì gì đó, thì ra em quên béng đi mất là lúc này ta đã chạy vòng for rồi, cụ thể là 2 vòng lồng for a (for b) từ 0, 1,..9.
Như thế ta đã có được giá trị a, b xác định ở mỗi cặp đôi vòng lặp a, b này và bắt đầu tìm c được bằng cách thay a,b vào cái đống q = (a^3 + b^3 -100a -10b) trong phương trình chuyển vế: c^3 - c + (a^3 + b^3 - 100a - 10b) = 0. Cái đống q này khi thay vào thì là hằng số rồi nên cứ chiếu theo Vieta, hoặc phương trình tổng hợp, lượng giác trên wiki mà anh có gửi, ở dạng: c^3 + pc + q = 0, với p = -1, q = a^3 + b^3 - 100a - 10b (q đã tính được cụ thể rồi) để bắt đầu công cuộc đi tìm c.
Ở chỗ vieta trên anh úp 2 hình trùng, nên đây là link để mọi người xem đầy đủ về vieta mà anh có nói: http://en.wikipedia.org/wiki/Cubic_e...s_substitution
OK, vậy là đã sáng tỏ!

@0852001, em quên nói rõ hơn ở về phần thứ 3 này, thực ra nó cũng chưa hẳn là phần giống như hai phần của mỗi nửa mảng trái, phải kia, mà nó thuộc vào phần mà mảng đó trước khi bị chia nhỏ (chia đôi) ra để giải quyết. Em sẽ nói rõ hơn như sau:
Giả sử mảng ban đầu của ta có dạng a[đầu..đuôi] với đầu là chỉ số đầu, đuôi là chỉ số đuôi.
Ta xác định một điểm giữa (lấy (đầu + đuôi)/2 chẳng hạn) và bắt đầu chia đôi mảng đó ra thành hai nửa là: a[đầu..giữa] (nửa trái) và a[giữa+1..đuôi] (nửa phải).
Như thế xuất hiện 3 tình huống khả nghi trong việc xác định mảng con lớn nhất cần tìm (gọi là mảng R đi cho gọn), đó là Mảng R này:

1. Nằm trọn trong nửa trái kia, tức là trong khoảng a[đầu..giữa]
2. Nằm trọn trong nửa phải kia, tức là trong khoảng a[giữa+1..đuôi]
3. Hoặc nằm gối đầu, tức là nằm trong khoảng a[đầu..đuôi], và dĩ nhiên mảng R phải đi qua điểm giữa.

Do đó, công việc trước hết cần làm là thực thi cái tình huống 3 ấy, (còn 2 tình huống 1 và 2, bản chất nó đệ quy, cứ chia đôi nhỏ ra, để rồi cũng đụng độ tình huống 3), tình huống 3 này là khi ta biết vị trí điểm giữa rồi, ta sẽ đi tìm mảng con lớn nhất của nửa trái a[đầu..giữa] và của nửa phải a[giữa+1..phải] rồi kết hợp kết quả từ 2 nửa đó lại.
Nôm na như thế này:
Tìm phần lớn nhất bên trái
Tìm phần lớn nhất bên phải
Kết hợp kết quả hai phần trên để tìm được phần lớn nhất có đi qua điểm giữa.
Gọi cái nôm na ở trên là TìmMảngGốiĐầu.

Và nôm na cho việc giải quyết cả bài toán TìmMảngConLớnNhất của chúng ta như sau.
TìmMảngConLớnNhất(đầu, đuôi) =
# TH mảng chỉ có 1 phần từ (Trường hợp cơ bản (dừng)) thì phần tử duy nhất đó cùng với chỉ số đầu, đuôi sẽ là mảng con lớn nhất R cần tìm
# Ngược lại:
+ Xác định điểm giữa = (đầu + đuôi)/2, rồi
Đệ quy TìmMảngConLớnNhất(đầu, giữa)
Đệ quy TìmMảngConLớnNhất(giữa + 1, đuôi), và
TìmMảngGốiĐầu(đầu, đuôi)

Ba cái TìmMảng... ở trên ta sẽ chọn ra cái lớn nhất, thì cái lớn nhất đó chính là thứ chúng ta cần tìm.

Ví dụ cho dễ hiểu hơn, ta có mảng A gồm 16 phần tử và cần đi tìm mảng R. Như vậy
TìmMảngConLớnNhất(0, 15) sẽ gọi TìmMảngConLớnNhất(0, 7), TìmMảngConLớnNhất(8, 15)
và rồi TìmMảngConLớnNhất(0, 7) sẽ gọi TìmMảngConLớnNhất(0, 3) và TìmMảngConLớnNhất(4,7)
và rồi TìmMảngConLớnNhất(0, 3) sẽ gọi TìmMảngConLớnNhất(0, 1) và TìmMảngConLớnNhất(2, 3)
và rồi TìmMảngConLớnNhất(0, 1) sẽ gọi TìmMảngConLớnNhất(0, 0) và TìmMảngConLớnNhất(1, 1)
...
lúc này TìmMảngConLớnNhất(0, 0) và TìmMảngConLớnNhất(1, 1) cả hai đều chỉ có một phần tử nên chiếu theo trường hợp cơ bản # ở trên sẽ trả về chính mảng chứa phần tử duy nhất đó. Rồi lúc này lại quay đầu đi TìmMảngGốiĐầu(0, 1) rồi so sánh với TìmMảngConLớnNhất(0, 0) và TìmMảngConLớnNhất(1, 1) (hai nửa của (0,1)) đã có được ngay trước đó để tìm được TìmMảngConLớnNhất(0, 1).
Cứ thế lại truy hồi tới trường hợp cơ bản để TìmMảngConLớnNhất(2, 3),.... rồi nào là so sánh để lựa ra cái lớn nhất.
Viết dài dòng như thế không biết mọi người có rõ không nữa.

[08520001]

[MENTION=11957]11520447[/MENTION]: Thông thường vét cạn là cách dễ hiểu, dễ code nhất. Tuy nhiên trong đa số trường hợp, nó chạy khá chậm. Vd bài này em duyệt n lần, mỗi lần duyệt, em duyệt thêm 1 số lần để tính tổng mảng con, cập nhật kết quả nữa. Thì số lần lặp sẽ rất lớn. Với n nhỏ

[09520019]

[*]Anh Châu ơi [MENTION=7969]09520019[/MENTION] anh có thể làm mẫu thử về việc giải phương trình bậc 3 với các ẩn tự do, em chưa hiểu ý anh nói lắm để hạ từ 3 vòng for xuống còn 2 vòng for.

thế này nhé: bài toán là a^3 + b^3 + c^3 = 100a + 10b + c
Bình thường chúng ta sẽ chạy 3 vòng for a,b,c để tìm nghiệm, tuy nhiên nếu để ý rằng ta chạy 2 vòng for thôi, thì ẩn còn lại sẽ trở thành 1 phương trình bậc 3. Mình thích chọn hệ số a b c nhỏ, nên chạy a và b, còn lại ẩn c, tức là

c^3 - c + (a^3 + b^3 - 100a - 10b) = 0 (I)

Đối với phương trình bậc 3 thì có công thức nghiệm. Công thức nghiệm này có thể tính trong O(1), cũng như công thức nghiệm pt bậc 2 vậy. Cho nên áp dụng công thức nghiệm thôi


(I) là phương trình bậc 3 tổng quát Ac^3 + Bc^2 + Cc + D = 0 với các hệ số A = 1, B = 0,C = -1, D = a^3 + b^3 - 100a - 10b (II)
ngoài ra nó cũng là phương trình bậc 3 suy biến c^3 + pc + q = 0 với p = -1 và q = a^3 + b^3 - 100a - 10b (III)

Nên bạn có nhiều lựa chọn:

http://en.wikipedia.org/wiki/Cubic_equation#Three_real_roots

Theo wiki, bạn có thể dùng cách giải tổng quát cũng được, nhưng khá dài.
Phương pháp Carnado là phương pháp dùng trong SGK, thường mình không dùng phương pháp này.

Thường thì mọi người thích phương trình suy biến hơn (III)

+ Carnado, dùng phương pháp này bạn chắc chắn tìm ra được 1 nghiệm, sau đó bạn chia đa thức cho đơn thức, tìm ra 2 nghiệm còn lại bằng phương trình bậc 2, hoặc cách khác là bạn tìm ra được 6 nghiệm, và thử lại 6 nghiệm này. Do đó mình mới đề xuất thêm Vieta
+ Vieta:
phương trình:
Đặt
Tức là ra phương trình
Nhân 2 vế với w^3
Đây là dạng phương trình bậc 2 của w^3. Tìm ra được nghiệm, thay vào cái phần đặt t hồi nãy.


Mấy cái phương pháp trên thì mệt nhất là lúc đụng vào số ảo, ưu điểm là không đụng lượng giác. Nhưng mà cách làm lượng giác thì nhanh và không phải lo số ảo. Nên hồi trước mình dùng công thức nghiệm bằng lượng giác cho nhanh ở wiki tiếng Việt http://vi.wikipedia.org/wiki/Ph%C6%B...b%E1%BA%ADc_ba

Đặt:



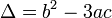
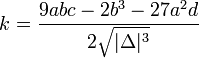
Xét 4 TH theo như wikipedia, cả 4 TH đều có công thức nghiệm sẵn, bạn cứ ráp vào là ra.

[12520244]

thấy mấy anh thảo luận sôi nổi quá, thấy thích ghê :byebye: giờ em mới để ý mấy thời gian lướt facebook, haivl vô ích quá, em thích code mà giờ trình độ vẫn bập bẹ :sad:, phải đầu tư thêm thôi, có gì mấy anh giúp đỡ em nha :funny:

[11520447]

@Tú: em có thể viết cụ thể hơn không?

Có học qua mấy cái chia để trị ji đó nhưng em ko biết áp dụng.
Nên gặp bài nào em cũng nghĩ ngay đến cách vẹn cạn
Bài này e nghĩ thế này :
- Số phần tử của dãy con tăng dần.
- Mảng có n phần thử thì duyệt n lần (mỗi lần duyệt sẽ có số phần tử trong mảng con khác nhau )
- bonus thêm cái hàm tính tổng mảng con đag xét, so sánh và lưu vào 1 biến kq

[08520001]

[MENTION=11756]11520246[/MENTION]: Thuật toán của em thiếu phần thứ 3 thì phải. Em mới nói 2 phần có được từ 2 mảng con trái và phải thôi. Thuật toán chia để trị này hay, nhưng ghi bằng tiếng Anh như vậy, anh sợ nhiều bạn không đọc. Nên em xem lại và ghi chi tiết để những bạn không đọc có thể hiểu được luôn nha. Thanks em.
Và mình khuyến khích các bạn sau khi hiểu 2 thuật toán này thì nên code bài này với cả 2 thuật toán này luôn.

[11520246]

• Anh Châu ơi [MENTION=7969]09520019[/MENTION] anh có thể làm mẫu thử về việc giải phương trình bậc 3 với các ẩn tự do, em chưa hiểu ý anh nói lắm để hạ từ 3 vòng for xuống còn 2 vòng for.
• Anh An [MENTION=7280]08520001[/MENTION] về bài của Tín em thấy cách anh đưa ra chính là thuật toán Kadane đã được đề cập ở Wikipedia - Maximum subarray problem, giải pháp đưa ra là duyệt toàn bộ mảng và dĩ nhiên độ phức tạp là vào khoảng tuyến tính O(n) với n là độ dài mảng.

Ngoài ra trên trang wiki trên cũng có nhắc đến một giải pháp khác là dùng Chia để trị để giải quyết bài toán Mảng con lớn nhất mà Tín đã giới thiệu. Em cũng xin chia sẻ thêm những gì đã tìm hiểu, đó là:
Ở đây ta phân chia vấn đề ra theo đúng nguyên tắc chia để trị, cụ thể là chia đôi ra, đại loại mục tiêu ở đây là "tìm mảng con lớn nhất của nửa trái mảng ban đầu", rồi lại "tìm mảng con lớn nhất của nửa phải mảng ban đầu", và rồi sẽ kết hợp lại để có được "mảng con lớn nhất". Như vậy từ mảng ban đầu ta cứ chia đôi ra, tìm mảng con lớn nhất ở mỗi bên, rồi gộp lại. Chắc chắc sẽ thực thi bằng đệ quy (giống như Merge Sort bình thường) với trường hợp cơ bản (dừng đệ quy) là khi mảng chỉ có 1 phần tử thì phần tử đó chính là max.

1. Như vậy ta sẽ thực thi một hàm tính tổng một mảng con (có chỉ số cho trước hẳn hoi). (Được một giá trị)
2. Bên cạnh đó ta chia mảng con đó ra làm hai, rồi tìm mảng con lớn nhất, cụ thể là của nửa mảng bên trái, nửa mảng bên phải (Được hai giá trị).
3. Sau đó so sánh và tìm max trong 3 giá trị trên, cứ thế truy hồi ngược trở về mảng có độ dài n ban đầu.
4. Tiếp tục đệ quy, vân vân vân.

Đại loại ý tứ là thế, cũng là do em có đọc được trong sách Introduction to Algorithms (Cormen, Leisserson,..), em có trích cho mọi người tiện đọc:
Trich-MangConLonNhat-Introduction_to_algorithms.pdf
Source Python, mọi người xem sẽ hiểu rõ hơn: max-subarray-divive-n-conquer.py
Làm mẫu chạy thử code:
Khai báo một mảng trong Python IDLE A = [2, 3, ,4 .....] tùy ý
Gọi hàm FindMaxSubArray(A,0, len(A) -1 ) sẽ trả về một bộ 3 thứ gồm: chỉ số đầu, chỉ số cuối, và giá trị của mảng con lớn nhất tìm thấy được.

[08520001]

@Châu: Anh nghĩ một đề bài không nên tồn tại quá lâu. bài đó đã xuất hiện từ qua tới giờ rồi, nhưng ít comment quá. Không biết trường mình có bao nhiêu bạn biết về thuật toán, yêu thích lĩnh vực này, mà theo tình hình này chắc cũng sẽ chìm vào quên lãng như nhưng topic trước.

Theo kinh nghiệm của mình thì đúng là thuật toán không quan trọng lắm khi ra trường vào làm ở đa số công ty phần mềm ở Việt Nam. Cho nên bạn nào nghĩ học thêm thuật toán để phục vụ sau này đi làm thì không cần tốn thời gian học nó nữa. Vậy học thêm thuật toán để làm gì trong khi nó vừa khó, vừa khô khan. Trước tiên, trong các khoa của CNTT thì có khoa Khoa học máy tính là có học và nghiên cứu về lĩnh vực này. Tuy nhiên, ở chương trình học ở Việt Nam, có thể nó không được thấy rõ, nhưng nếu đi du học về ngành này thì sẽ thấy, yêu cầu khá cao. Ví dụ có một cuộc phỏng vấn của google, trong đó có một câu thuật toán yêu cầu giải một bài toán thuộc lĩnh vực cấu trúc dữ liệu nâng cao, làm và viết code trong 15 phút. Theo mình thấy thì đó là khó. Ngoài ra, học thuật toán, làm các bài tập về thuật toán, sẽ giúp hiểu rõ về ngôn ngữ hơn. Vì hiện nay có rất nhiều ngôn ngữ, khi chúng ta học một ngôn ngữ, và muốn luyện tập để thành thạo ngôn ngữ đó, thì chúng ta luyện tập bằng cách nào ngoài các làm bài tập, những bài tập đó thuộc về thuật toán. Bài tập càng phức tạp thì càng đòi hỏi phải thành thạo ngôn ngữ. Tiếp theo, học thuật toán giúp rèn luyện tư duy về phân tích, xử lý các vấn đề nhỏ thiên về kĩ thuật trong các project. Thuật toán tốt thì nhanh chóng tìm ra được solution phù hợp và chính xác, code viết ra sẽ rõ ràng, dễ hiểu, còn có thể cải tiến về tốc độ.
Đó là những ý kiến của mình về việc học thuật toán để giúp các bạn hiểu thêm về lĩnh vực này. Hàng năm có các kì thi thuật toán như Olympic Tin học sinh viên, kì thi lập trình quốc tế ACM-ICPC, trường mình đều có tham gia, và có kế hoạch ôn luyện. Nhưng năm nay, tới thời điểm này thì chưa thấy tổ chức ôn luyện. Trong những năm qua, dù có phổ biến nhưng thuật toán vẫn chỉ là 1 khái niệm mơ hồ, không đáng quan tâm của đa số sinh viên trường mình. Mình thấy đây là điều đáng buồn vì trường mình là trường Đại học Công nghệ thông tin.

[09520019]

- Không nên đánh giá độ khó của bài toán.
- Nên kích thích tính tò mò, giải quyết vấn đề độc đáo của các bạn.

tăng sự hứng thú code, bị thách thức bởi một cái gì đó.

Về việc kích thích sáng tạo với trí tò mò thì a không có gì để phản đối, anh chỉ theo hướng khác em thôi Với những dạng bài như thế này thì thách thức mà anh thường đặt ra là code nhanh (tầm 1~3' là xong), pass hết test. Code ngắn, đẹp, gọn, súc tích . Đó cũng là 1 thách thức lớn, vì đối với những người quen với tư duy tối ưu sẽ gặp trục trặc, thường sẽ tốn tầm 10' cho bài này Nói chung là ý của em thì không có vấn đề gì lớn. Chỉ là anh giải thích cho em thấy tại sao anh An lại chấp nhận đáp án và đi tiếp

Không sao em. Đó là tâm sự của 1 sinh viên yêu thích thuật toán mà.
Quay lại với bài toán, a có ý tưởng như sau:
Đặt current_sum là tổng hiện tại, max_sum là tổng lớn nhất
Duyệt qua dãy, với mỗi số, ta cộng dồn vào current_sum. Nếu current_sum < 0 thì ta gán lại current_sum = 0. Ngược lại current >= 0, ta so sánh với max_sum và cập nhật lại max_sum = max(max_sum, current_sum)

Anh giải thế thì còn ai giải nữa :-w

[08520001]

Không sao em. Đó là tâm sự của 1 sinh viên yêu thích thuật toán mà.
Quay lại với bài toán, a có ý tưởng như sau:
Đặt current_sum là tổng hiện tại, max_sum là tổng lớn nhất
Duyệt qua dãy, với mỗi số, ta cộng dồn vào current_sum. Nếu current_sum

[10520100]

@ anh Châu : Lời giải hoàn hảo ! Đúng là k uổng công e ngưỡng mộ a Châu.

Hề hề, mà anh Châu lại lái ý của em đi qua hướng khác rồi. Điều em mong muốn ở đây đã thể hiện rất rõ :

- Không nên đánh giá độ khó của bài toán.

- Nên kích thích tính tò mò, giải quyết vấn đề độc đáo của các bạn.

Em đâu dám đề cập đến Olimpic hay ACM gì đâu Cả đời chưa được đi thi một lần, lấy gì mà đề cập

Theo em thấy, ở cái thời điểm Facebook, Haivl, Internet gây bão thì cách kích thích tính tò mò, sáng tạo của các bạn là tốt nhất. Chỉ có vậy mới mong các bạn giảm thời gian game, và tăng sự hứng thú code, bị thách thức bởi một cái gì đó.

Cũng giống như thời cấp 3, tụi em thường mua báo Toán học tuổi trẻ để giải, nộp những bài trong đó. Những bài mà kì thi đại học không bao giờ ra thì tụi em vẫn làm.
Bởi vì mỗi người đều yêu thích cảm giác giải được bài trong đó.
giờ code cũng vậy, tự thách thức mình hay gọi là "tự sướng" cũng được, giúp ta code vui hơn, sâu hơn và có cái tâm của nghề IT hơn.

Em xin hết ạ, hi vọng a An thông cảm vì đã làm loãng topic.